II lavoro di analisi statistica che il compilatore dei test deve svolgere non termina con la redazione della stesura definitiva del test. Occorre effettuare tutta una serie di rilevazioni che permettano di interpretare correttamente i punteggi ricavati dalla somministrazione del test ai gruppi di allievi. Per giudicare la difficoltà globale del test, l'ampiezza del "ventaglio" di punteggi, il grado di concordanza dei risultati del test con altre serie di risultati, il valore da attribuire ai singoli punteggi, è necessario calcolare una serie di indici e parametri. Il primo e più semplice di essi è la media aritmetica, che tutti ben conosciamo anche perché nella prassi scolastica a fine trimestre o quadrimestre si "fanno le medie" per determinare il voto.

La media aritmetica (M) si ottiene dividendo la sommatoria (Σ) dei punteggi (x) per il numero (N) dei punteggi stessi:

M = Σ x / N

II calcolo del punteggio medio conseguito dagli allievi in un test ci offre un primo termine di raffronto: anzitutto ci permette di osservare quali allievi abbiano fornito una prestazione superiore alla media e quali invece una prestazione inferiore; in secondo luogo possiamo assumere la media aritmetica come indice della difficoltà globale di un test. Una prova in cui il punteggio medio (espresso su una scala di cento punti) è pari a 58 è, globalmente considerata, assai più diffìcile di un test la cui media aritmetica dei punteggi (sempre riportata a 100) è pari a 90. Di conseguenza, i punteggi grezzi hanno tutti un valore relativo. L'allievo che consegue un punteggio di 78 nel primo test si colloca ben al di sopra della media, mentre lo stesso punteggio nel secondo test potrebbe equivalere ad una prestazione scadente.

La media aritmetica possiede un'importante proprietà: se si sommano algebricamente gli scostamenti (ossia le differenze) di ciascun punteggio dalla media, il totale è uguale a zero. Ricorriamo ad un semplice esempio per chiarire il concetto.

Si abbiano i punteggi: 2, 4, 7, 11; la media aritmetica è:

M = (2+4+7+11) / 4 = 24 / 4 = 6

Gli scostamenti saranno: 2—6 = —4; 4—6 == —2; 7—6 = 1; 11—6 =5, e la loro somma algebrica:

In una serie di punteggi (ordinati dal migliore al peggiore) la mediana (ME) corrisponde al punteggio centrale. Esempio: si abbiano i punteggi 82, 47, 41, 38, 29, 28, 24. La mediana è 38, essendo questo il punteggio centrale della scala, preceduto e seguito da altri tre punteggi. Qualora i punteggi fossero di numero pari (non esiste in tal caso un punteggio centrale), si assume convenzionalmente come mediana la media dei due punteggi centrali; ad esempio, con i punteggi 40, 38, 35, 31, 30, 22, la mediana è

(35 + 31) / 2 = 33

Calcolando la media aritmetica per i due esempi precedenti, si può verificare che media e mediana corrispondono spesso a valori diversi; dell'utilità e della funzione della mediana ci occuperemo in seguito.

La frequenza di un dato statistico corrisponde al numero delle volte in cui tale dato compare in una certa rilevazione. Se in un test 5 allievi hanno conseguito il punteggio 36, si dirà che 5 è la frequenza di tale punteggio. Negli esempi che abbiamo preso in considerazione finora (per il calcolo di medie e mediane) ciascun punteggio appariva una sola volta, ossia la sua frequenza (f) era uguale a 1. Se i singoli punteggi hanno frequenze diverse da 1, per il calcolo della media aritmetica occorre anzitutto moltiplicare ogni punteggio per la rispettiva frequenza, indi sommare i prodotti e dividere il totale per il numero globale dei punteggi. La formula data in precedenza per il calcolo della media aritmetica deve essere così modificata:

M = Σfx / N

Questa media si chiama ponderata perché ciascun dato viene moltiplicato per il suo "peso" (pondus) prima di essere immesso nella formula.

La moda è il dato che presenta la massima frequenza; nei test, è il punteggio conseguito dal maggior numero di allievi.

La media, la mediana e la moda sono misure di tendenza centrale: per loro natura tendono infatti a collocarsi al centro di una graduatoria o di una serie di punteggi.

Per rilevare la moda e calcolare la media ponderata conviene di solito ordinare i dati sotto forma di tabella. Nella prima colonna si riportano i punteggi conseguiti in un test, nella seconda le frequenze di ciascun punteggio e nella terza i prodotti dei punteggi per le rispettive frequenze. La seguente tabella riporta i dati ricavati dalla somministrazione di un test a cento allievi:

Inserendo i dati nella formula, otteniamo M = 1880 / 100 = 18,8; la moda si ricava direttamente dalla colonna delle frequenze: poiché il punteggio 20 è stato conseguito dal maggior numero di allievi, esso costituisce la moda per quel test. Il calcolo della mediana, in situazioni come questa, presenta qualche difficoltà; per i nostri scopi potrà tuttavia bastare un valore approssimato, desunto dalla distribuzione delle frequenze. Sommando progressivamente le frequenze iniziando dall'alto, riscontriamo che il cinquantesimo e il cinquantunesimo posto in graduatoria sono entrambi occupati da allievi che hanno conseguito il punteggio 19; questo punteggio può quindi essere assunto come valore mediano.

Un'ultima misura di tendenza centrale da prendere in esame (ci servirà in seguito) è la media quadratica, che è la radice quadrata della media aritmetica dei quadrati dei dati:

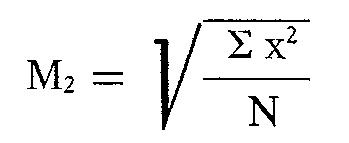
In pratica, si calcolano i quadrati dei dati e si sommano; il totale viene diviso per il numero dei dati, indi si estrae la radice quadrata del quoziente ottenuto. Il vantaggio principale della media quadratica consiste nell'eliminazione dei segni negativi; infatti qualsiasi numero, positivo o negativo, diventa positivo quando viene elevato al quadrato.

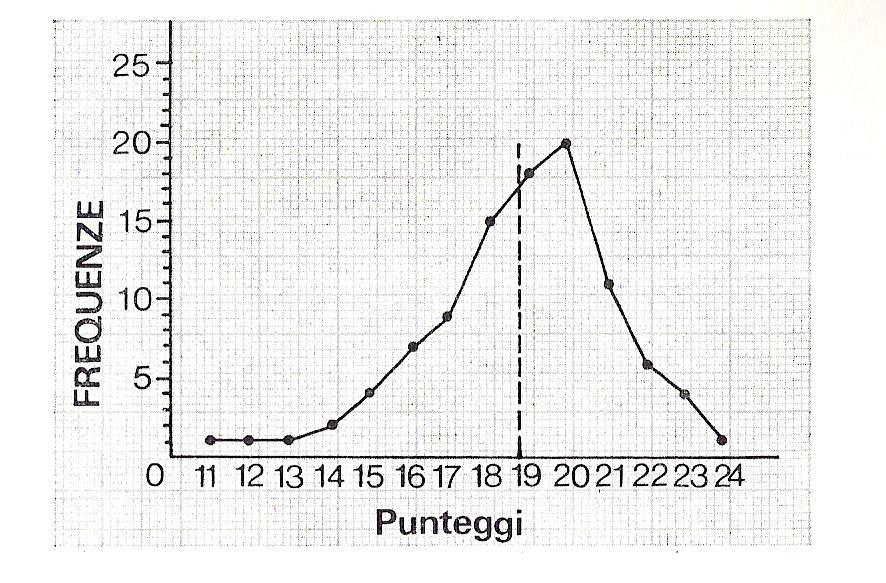
Possiamo rappresentare graficamente l'andamento dei dati riportati alla tabella precedente, ottenendo il poligono delle frequenze: l'asse orizzontale del grafico (ascissa) reca i punteggi; l'asse verticale (ordinata) le frequenze.

La linea tratteggiata verticale, in corrispondenza del punteggio 18,8, rappresenta la media aritmetica. Il grafico mette in evidenza come la maggioranza degli studenti abbia conseguito un punteggio superiore alla media; ne è conferma il fatto che il valore della mediana è più alto del valore della media.

Indagini statistiche a vasto raggio hanno dimostrato che se la popolazione considerata è sufficientemente numerosa le frequenze relative a dati antropometrici o psicometrici si distribuiscono secondo una tipica curva a campana che, dal nome del matematico che per primo ne mise in evidenza le proprietà, prende il nome di curva di Gauss. I dati antropometrici sono la statura, il peso, la circonferenza toracica, ecc.; i dati psicometrici sono, ad esempio, i quozienti d'intelligenza, ma anche i punteggi dei test di profitto tendono a distribuirsi secondo lo stesso modello matematico.

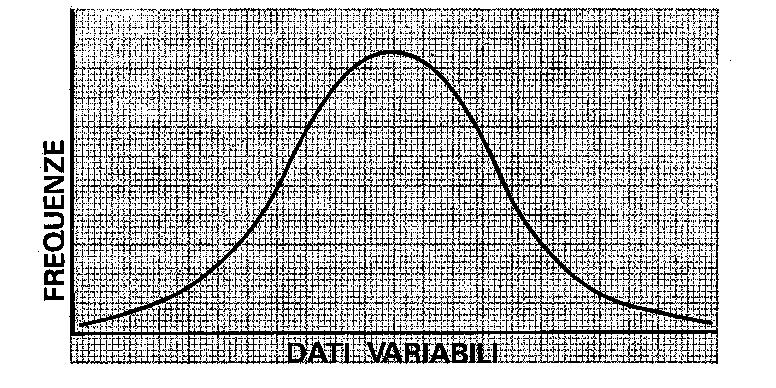
Rispetto ai poligoni delle frequenze che possiamo ricavare da un numero limitato di dati, la curva gaussiana presenta alcune notevoli e caratteristiche differenze. Anzitutto, media, mediana e moda coincidono: il dato medio è anche il più frequente, e divide la popolazione in due parti uguali. Se, ad esempio, la statura media dei giovani alla visita di leva, in un certo anno, è cm. 170, il gruppo dei giovani alti cm. 170 è più numeroso di ogni altro gruppo, ed i giovani la cui statura supera tale dato equivalgono per numero a quelli la cui statura è inferiore alla media.

Inoltre, la curva è simmetrica, il che significa che le frequenze diminuiscono in pari misura — quando ci allontaniamo dal dato medio — sia nella direzione dei valori bassi che in quella dei valori alti. Così, ad esempio, il gruppo dei giovani alti cm. 200 (cm. 30 più della media) tende ad essere altrettanto numeroso del gruppo dei giovani alti cm. 140 (cm. 30 meno della media).

Osservando l'andamento della curva, da sinistra verso destra, notiamo che essa all'inizio è concava verso l'alto, poi è convessa per tutta la parte centrale, indi è nuovamente concava verso l'alto. I punti in cui la curva cambia direzione (punti di flesso) hanno notevole importanza per la determinazione della variabilità. Con questo termine indichiamo la possibilità che hanno i valori di disporsi in una gamma più o meno estesa. Nell'esempio da noi considerato, i punteggi variavano da 11 a 24; una variabilità maggiore avrebbe dato luogo ad un poligono più largo, una variabilità minore ad un poligono più stretto. Ritornando alla curva normale, se riportiamo sull'ascissa i punti di flesso A e B e rileviamo a quali dati corrispondono (rispettivamente A' e B'), disponiamo di un dato preciso sulla variabilità dei dati.

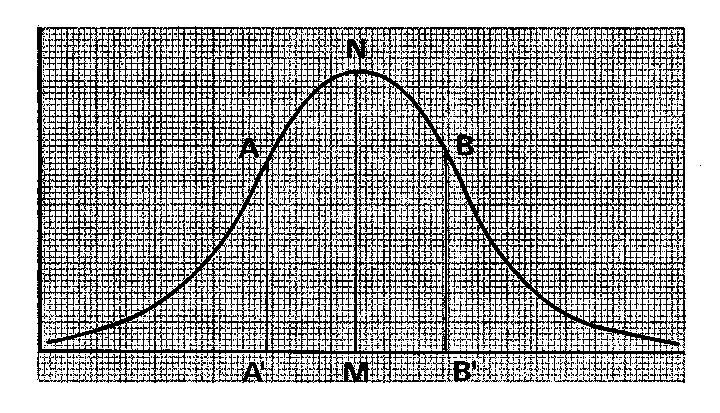
Il dato, chiamato deviazione standard, corrisponde all'intervallo tra il valore di M e quello di A oppure B'. Ad una deviazione maggiore corrisponde una curva più larga, ad una deviazione minore una curva più stretta; esse rappresentano rispettivamente una dispersione verso i valori estremi e una concentrazione verso il valore medio. La deviazione standard può essere calcolata, per ogni serie di dati, abbastanza agevolmente per mezzo della formula apposita (v. paragrafo 10.4).

Prima però di passare al calcolo del suo valore occorre approfondire il significato della determinazione dei punti-chiave in una distribuzione normale delle frequenze. È stato calcolato che nell'area compresa tra AA' e BB' si concentra il 68% circa della popolazione; convenzionalmente si attribuisce a questo nucleo centrale la denominazione di norma. Al difuori della norma si colloca quindi il 16% della popolazione con i dati più bassi (nel caso della statura, i nani o comunque le persone notevolmente basse) ed il 16% della popolazione con i dati più alti (i giganti o le persone notevolmente alte).

Nella figura seguente la deviazione standard è stata riportata esternamente una seconda volta in entrambe le direzioni:

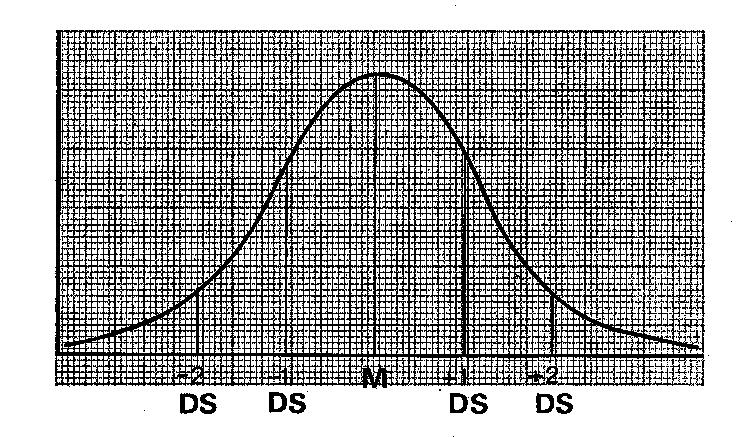
Sulla scala dei dati si sono quindi calcolati cinque punti importanti: —2 DS, ossia due volte la deviazione standard in senso negativo; —1 DS, una deviazione standard in senso negativo; M, il valore della media aritmetica; +1 DS, una deviazione standard in senso positivo; +2 DS, il doppio della deviazione standard in senso positivo. Nell'area compresa tra le ascisse corrispondenti a 2 DS (in altre parole, tra le due linee verticali esterne) si colloca il 96% circa della popolazione; all'esterno troviamo quindi il 2% dei dati più bassi ed il 2% dei dati più alti.

Ritorniamo all'esempio della statura e supponiamo di aver calcolato che la deviazione standard è pari a cm. 10. Ne deduciamo che:

a) il 68% dei giovani di leva ha una statura compresa tra cm. 160 (170—10) e cm. 180 (170+10);

b) il 96% di essi ha una statura compresa tra cm. 150 (170—2x 10) e cm. 190 (170+2x10);

c) su un campione rappresentativo di 100 soggetti, un giovane alto cm. 180 supera per statura 84 soggetti, ed è superato da 16;

d) raffrontato allo stesso campione, un giovane alto cm. 150 supera per statura 2 soggetti, ed è superato da 98; analogamente si procede per gli altri punti considerati.

L'indice che riporta i singoli dati su una scala teorica di cento soggetti, tenuto conto della distribuzione normale delle frequenze, si chiama centile. Per le ragioni sopra considerate, al valore della media aritmetica corrisponde il centile 50; a +1 DS il centile 84; a +2 DS il centile 98; a —1 DS il centile 16; a —2 DS il centile 2.

Quale sarà (sempre riferito all'esempio precedente) il centile di un giovane alto cm. 175? Occorre anzitutto calcolare la differenza tra il dato e la media, indi dividere per la deviazione standard:

questo calcolo ci fornisce il punto Z relativo al dato considerato.

Z = (x—M) / DS = (175—170) / 10 = 0,5

Un'apposita tabella permette di ricavare il centile corrispondente al punto Z; nell'esempio considerato, troviamo il valore 69,15, che significa che la statura di cm. 175 fa sì che quel giovane superi altri 69 soggetti e sia superato da 31.

Il calcolo dei centili ci permette quindi di ottenere un parametro per la corretta interpretazione di qualsiasi dato o punteggio. All'inizio del capitolo avevamo accennato al valore relativo dei punteggi; evidentemente, se anziché raffrontarli alla sola media aritmetica possiamo valutarli alla luce di altri indici, usciamo dal vago e dal generico. Il confronto tra dati assoluti non tiene conto della variabilità: un punteggio che supera la media, ad esempio, di 20 punti (su una scala di 100) può essere ottimo o appena discreto a seconda che la deviazione standard sia rispettivamente pari a 8 o a 40.

Il centile è anche un dato di raffronto tra i punteggi ottenuti dallo stesso allievo in test diversi; non è altrimenti possibile confrontare il punteggio 85 ottenuto nel test A con il punteggio 73 ottenuto nel test B, anche sapendo che la media aritmetica è pari a 80 nel primo e a 70 nel secondo.

Data una serie di dati o punteggi, la deviazione standard equivale alla media quadratica degli scostamenti dalla media aritmetica, ed è espressa dalla formula:

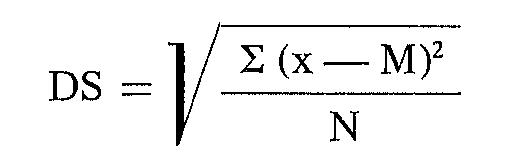
Analiticamente, la procedura è la seguente:

1) calcolare la media aritmetica (M);

2) sottrarre la media aritmetica da ciascun punteggio, per ottenere gli scostamenti (x — M);

3 ) elevare al quadrato gli scostamenti (x — M)²;

4) sommare i quadrati degli scostamenti: Σ (x—M)²;

5) dividere la sommatoria per il numero dei punteggi N;

6) estrarre la radice quadrata.

Questa procedura si applica quando tutti i punteggi ricorrono una sola volta (ossia la frequenza è uguale a 1); in caso contrario, prima di sommare i quadrati degli scostamenti, occorrerà moltipllcare ciascuno di essi per la rispettiva frequenza.

Ancora una volta, il modo migliore di procedere consiste nel predisporre una tabella riportando tutti i dati occorrenti: completeremo quindi la tabella iniziale con altre tre colonne calcolando gli scostamenti dalla media, i quadrati degli scostamenti, ed i prodotti dei quadrati per le rispettive frequenze:

Poiché la tabella, a prima vista, potrebbe apparire più complicata di quanto essa in effetti non sia, sarà bene chiarire che:

a. le prime tre colonne sono identiche a quelle della tabella precedente;

b. la quarta colonna reca i risultati ottenuti sottraendo 18,8 (che è il valore della media aritmetica) a ciascun punteggio: 23—18,8 = 4,2; 17—18,8 = —1,8, e così via;

c. la quinta colonna è costituita dai quadrati dei numeri della quarta colonna: il calcolo è estremamente facile e rapido disponendo di comunissime tavole numeriche;

d. nell'ultima colonna sono riportati i prodotti ottenuti moltiplicando i quadrati (quinta colonna) per le rispettive frequenze (seconda colonna). La sommatoria di questi prodotti va inserita nella formula per il calcolo della deviazione standard:

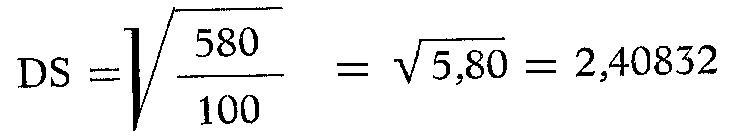
II risultato (anch'esso desunto dalle tavole numeriche, senza bisogno di effettuare l'operazione di estrazione della radice quadrata) si può arrotondare a 2,41.

Questo dato, unitamente alla media aritmetica, ci serve per valutare il valore di ciascun punteggio e, eventualmente, per calcolare il centile. Sottraendo la deviazione standard alla media, ad esempio, troviamo il punteggio che corrisponde a —1 DS, e che a sua volta corrisponde al centile 16. Nel nostro caso avremo 18,8—2,41= 16,39: secondo le percentuali calcolate sulla base della curva teorica, al disotto di tale punteggio si dovrebbe trovare circa il 16% dei soggetti. In effetti, se sommiamo il numero di allievi che hanno un punteggio inferiore a 16,39, troviamo che essi sono sedici (su un totale di 100).

Allo stesso modo, possiamo calcolare + 1 DS: 18,8 + 2 41 = 21,21. Al punteggio 21 dovrebbe quindi corrispondere il centile 84: effettivamente possiamo osservare che gli allievi che hanno conseguito quel punteggio occupano nella graduatoria (a pari merito) i posti dal 12° al 22°, e assumendo come valore centrale il 17° posto in graduatoria, si vede come vi sia una notevole vicinanza tra i dati teorici e quelli reali, tenuto anche conto della parte decimale.

Non dobbiamo tuttavia attenderci una corrispondenza perfetta tra la distribuzione delle frequenze nel campione e quella normale espressa dalla curva di Gauss: tale corrispondenza si ha solo con un campione sufficientemente ampio, omogeneo ed equilibrato, mentre nel nostro caso già il poligono delle frequenze denunciava una distribuzione asimmetrica rispetto al valore medio. Ciò spiega come mai, ad esempio, riscontriamo 73 punteggi su 100, invece dei 68 prevedibili, compresi nell'area centrale tra —1 DS e +1 DS ossia tra 17 e 21.

Desiderando calcolare per i punteggi di un test centili attendibili, che possano servire da punto di riferimento per chiunque riutilizzerà il test standardizzato, bisogna effettuare la taratura su un notevole numero di soggetti, così da ottenere un poligono delle frequenze che si avvicini abbastanza alla curva teorica. Nelle normali situazioni scolastiche ciò si realizza difficilmente, e quindi i dati raccolti mediante l'elaborazione dei punteggi vanno opportunamente interpretati.

Il centile, pur rappresentando una misurazione del profitto molto più accurata rispetto al punteggio grezzo fornito da un test, non può di per sé tradursi in un voto convenzionale. Anzitutto occorrerebbe aver precisato ove collocare il livello di sufficienza: se questo viene fatto coincidere con il limite inferiore della norma, al centile 16 può già corrispondere il voto 6. È quindi totalmente assurdo pensare che si possa far corrispondere al centile 80 il volo 8, o al centile 30 il voto 3. Così facendo si dimostrerebbe di non aver capito nulla sulla distribuzione normale delle frequenze; inoltre si avrebbe una preponderanza di voti negativi, dato che al valore medio (centile 50) verrebbe assegnato un 5. Portando il discorso ad un livello più generale, occorre richiamare la distinzione basilare tra valutazione dell'allievo e misurazione del profitto, e mettere in guardia contro ogni tentativo di "meccanizzare" i giudizi.

L'uso corretto dei centili (così come di tutti gli altri dati statistici) consiste nell'impiegarli per verificare i progressi di ogni allievo, o evidenziare le lacune di preparazione per intervenire con una strategia didattica che permetta di condurre lo studente a superarle. In altre parole, la maggior precisione delle misurazioni deve tradursi in un migliore impegno didattico, e non già in un alibi per un atteggiamento selettivo che pretenderebbe di trovare una giustificazione nei risultati "oggettivi" di un test.

Tutti gli strumenti di misurazione del profitto e di valutazione, siano essi test oggettivi o prove tradizionali, conducono all'attribuzione di classificazioni (voti, punteggi, ecc.) e/o alla formazione di graduatorie. Può essere quindi necessario rispondere a domande come le seguenti:

— In quale misura i risultati della prova A sono confermati da quelli della prova B, ovvero sono in contrasto con essi?

— I punteggi ricavati dalla somministrazione di un test sono, in complesso, compatibili con gli altri dati in possesso dell'insegnante?

La risposta a queste domande è di primaria importanza: se si dovesse accertare che i dati forniti da un test non hanno alcuna conferma negli altri elementi di giudizio a disposizione dell'insegnante, ovvero sono contraddetti da prove analoghe sicuramente affidabili, ciò significherebbe che il test è privo di validità. In tal caso non bisogna tenere conto dei risultati di quel test, che deve essere revisionato radicalmente.

Per risolvere questi problemi la statistica ha elaborato una serie di formule per il calcolo dell'indice di correlazione (r), che esprime il grado di corrispondenza esistente tra due serie di dati. L'indice è espresso da un numero compreso tra +1,00 e —1,00. Al valore di +1,00 corrisponde una correlazione diretta perfetta, come quella che intercorre tra il peso e il peso specifico di una serie di oggetti (a parità di volume); a —1,00 equivale una correlazione perfetta inversa, come quella tra le velocità ed i tempi necessari per percorrere un dato tragitto; lo zero indica l'assenza di correlazione tra le due serie di dati prese in esame.

Il concetto di correlazione non deve essere confuso con quello di causalità. Se si confrontano i dati annuali relativi all'andamento delle morti per annegamento con quelli sull'andamento annuo delle vendite dei gelati, si riscontra un'alta correlazione positiva, senza che peraltro uno dei due fenomeni sia la causa (o l'effetto) dell'altro: una terza variabile, il caldo, è la verosimile causa di entrambi.

Il metodo più semplice per il calcolo di r sì basa sulle differenze di posizione nelle due graduatorie (rank difference method di Spearman). Dopo aver riordinato gli studenti dal migliore al peggiore in base ai punteggi (separatamente per le due graduatorie), si attribuiscono a ciascuno le posizioni in classifica: al migliore 1, al secondo 2, e così via. Nel caso di studenti a pari merito, si fa la media delle posizioni occupate: se il terzo ed il quarto hanno lo stesso punteggio, attribuiremo ad entrambi 3,5; se il sesto, il settimo e l'ottavo sono a pari merito, avranno tutti la posizione 7. Fatto ciò con entrambe le graduatorie, si confrontano le posizioni, studente per studente, e si calcolano le differenze. Se l'allievo A è ottavo nella prima graduatoria e decimo nella seconda, la differenza (D) è 2. Non occorre indicare se sia +2 o —2, perché l'operazione successiva consiste nell'elevare le differenze al quadrato, e con ciò (come abbiamo già visto) si eliminano i segni negativi.

La sommatoria dei quadrati delle differenze di posizione viene inserita nella seguente formula:

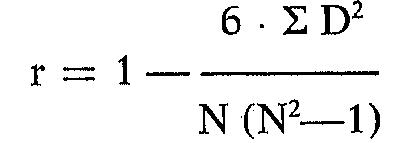
in cui D indica le differenze di posizione in graduatoria e N il numero dei soggetti.

Illustriamo la procedura con un esempio, basato sui risultati conseguiti da un gruppo di sette allievi in due test. Accanto a ciascuno indichiamo: il punteggio nel primo test (x), il punteggio nel secondo test (y), la posizione in graduatoria nel primo test (gx) e nel secondo (gy), la differenza di posizione in graduatoria (D) ed il suo quadrato (D²).

La sommatoria dei dati dell'ultima colonna (Σ D2 = 20,50), assieme al numero degli allievi (N=7), può ora essere immessa nella formula:

r = 1 – (6 x 20,50) / 7(7²—1) = 1 - 123 / 7(49—1) = 1- 123 / 7 x 48 = 1 – 123 / 336 = 1-0,36=0,64.

Poiché normalmente si assume 0,40 come indice minimo accettabile di correlazione positiva, possiamo ritenere la correlazione tra i le due graduatorie discreta ma non altissima. Vi sono infatti alcuni I casi notevoli di dissimmetria: ad esempio, l'allievo C, secondo a i pari merito nel primo test, è penultimo nel secondo; l'allievo D, secondo nel secondo test, è solo quarto nel primo. In alcuni casi la formula di Spearman non basta a darci un indice esatto della correlazione tra due serie di punteggi. Nell'esempio seguente:

la correlazione tra le graduatorie è perfetta, e quindi dalla formula ricaviamo r = l,00. Osservando i punteggi si rilevano invece delle dissimmetrie: i valori della prima serie sono distribuiti irregolarmente su un arco molto esteso (da 1 a 9); quelli della seconda serie si collocano ad intervalli regolari e in un arco molto più ristretto. Calcolando il coefficiente di correlazione sulla base dei punteggi (product-moment correlation di Pearson) si ottiene r= 0,945, un indice molto alto ma che evidenzia come la correlazione non sia perfetta.

La formula per il calcolo di questo indice è:

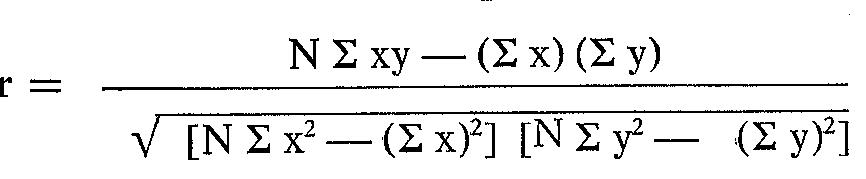
In questa formula, oltre a N (numero degli allievi) vanno immessi i seguenti dati:

a) la sommatoria dei punteggi del primo test: Σ x;

b) la sommatoria dei punteggi del secondo test: Σ y;

c) la sommatoria dei quadrati dei punteggi del primo test: Σ x²;

d) la sommatoria dei quadrati dei punteggi del secondo test: Σ y²;

e) la sommatoria dei prodotti ottenuti moltiplicando ciascun punteggio x per il corrispondente punteggio y: Σ xy;

f) il quadrato della sommatoria delle x: (Σ x)²;

g) il quadrato della sommatoria delle y; (Σ y)².

Anche in questo caso il ricorso ad una tabella si rivela utile e serve a chiarire che anche questo calcolo, sebbene più laborioso dell'altro, non è però più difficile. Utilizzeremo ancora i dati impiegati per il calcolo dell'indice di Spearman:

Inserendo le sommatorie nella formula otteniamo:

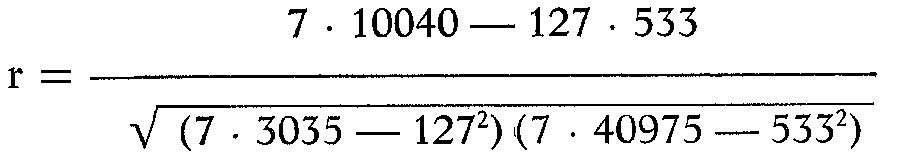
da cui, svolgendo i calcoli, si ricava r = 0,69.

La differenza (peraltro contenuta nei limiti di un 5%, valore relativamente modesto) tra i risultati forniti dalle due formule è da porre in relazione alla diversità dell'oggetto rilevato.

Si noti che con questa seconda formula si possono confrontare direttamente tra di loro due serie di dati, prescindendo dalla scala su cui essi si collocano: ciò permette, tra l'altro, di raffrontare i punteggi di un test (in centesimi o in qualsiasi altra scala) con i tradizionali voti in decimi. La possibilità di scegliere tra due formule diverse deve essere sfruttata a seconda degli obiettivi che ci poniamo nell'effettuare l'indagine statistica.

Non possiamo ignorare che l'impiego dei test nella normale routine di insegnamento ha suscitato e suscita varie perplessità ed obiezioni. Ad alcune di esse, pensiamo di avere dato una risposta trattando dei singoli problemi; altre, che spesso ci vengono presentate dagli insegnanti, meritano di essere trattate specificamente. Ad esse dedichiamo queste pagine conclusive.

È vero. Molto di questo tempo viene però recuperato attraverso una più rapida somministrazione e correzione delle prove, e ciò costituisce anche un vantaggio dal punto di vista didattico nella misura in cui si riesce a comunicare sollecitamente agli allievi il risultato delle prove sostenute e la correzione degli errori. Le più comuni prove tradizionali richiedono tempi relativamente lunghi per essere corrette e accade spesso che gli elaborati vengano riconsegnati agli allievi quando questi hanno dimenticato la genesi dei propri errori e quindi sono interessati essenzialmente al voto. Si tenga poi presente che il tempo impiegato per redigere un test è inversamente proporzionale all'esperienza acquisita in questa attività: le prime volte si procede lentamente e con difficoltà, ma in seguito l'abitudine permette di preparare prove abbastanza complesse anche senza molto tempo disponibile.

È solo parzialmente vero. In quanto alla difficoltà e al dispendio di tempo, vale ciò che abbiamo appena osservato a proposito della redazione dei quesiti: dopo le prime volte, l'applicazione delle formule diventa agevole e relativamente rapida. Si consideri poi che non occorre percorrere ogni volta l'intero itinerario di rilevazioni ed elaborazioni statistiche; ciò è indispensabile solo per la preparazione di test standardizzati. Spesso può bastare il calcolo della media aritmetica e della deviazione standard. Abbiamo preso in considerazione alcune formule (tralasciandone peraltro numerose altre) sopratutto per illustrare l'ampia gamma di informazioni che si ricavano da un'analisi statistica e per puntualizzare alcuni concetti essenziali, quali quelli di validità e affidabilità dei test, distribuzione delle frequenze e correlazione. Per i calcoli occorrono le tavole numeriche dei quadrati e delle radici quadrate; disponendo di una calcolatrice, o anche solo di un'addizionatrice tascabile, si può accelerare notevolmente l'esecuzione dei conteggi.

Non è vero. Un ciclostile e (per i test orali) un magnetofono sono, in linea di massima, tutto quello che occorre; non crediamo che, nella situazione attuale delle scuole italiane, sia eccezionale il disporne.

È vero qualora i test debbano servire ad un impiego generalizzato su vasta scala: è il caso dei test di profitto posti in commercio. Altrimenti ciascun insegnante non solo può, ma deve prepararsi i "suoi" test, che vanno bene nelle "sue" classi, esattamente come predispone le prove tradizionali. Naturalmente la collaborazione di altri insegnanti può essere preziosa e contribuire ad evitare errori di impostazione del test, redazione dei quesiti e interpretazione dei risultati.

È vero. Tranne alcune eccezioni, le Facoltà di Lingue Straniere non hanno ancora dato adeguato spazio alla linguistica applicata, alla psicolinguistica, ed alla metodologia e didattica delle lingue straniere. L'obiezione quindi si riferisce non al LT come tale, bensì alla preparazione professionale complessiva dell'insegnante di lingue straniere. Coloro che invece possiedono sufficienti nozioni linguistiche e metodologiche non incontrano particolari difficoltà ad affrontare la problematica del testing.

È vero. Del resto non abbiamo mai affermato che i test debbano soppiantare in toto le prove tradizionali: essi servono invece ad assicurare che tali prove vengano affrontate dagli allievi in condizioni ottimali. Far eseguire un riassunto o una composizione dopo aver accertato la padronanza delle strutture linguistiche è assai più produttivo che servirsi delle stesse prove anche per verificare tale padronanza.

Non è vero: ciò potrebbe accadere solo qualora si confondesse la verifica delle abilità (che è un aspetto della misurazione del profitto) con la valutazione dell'allievo: abbiamo già operato una netta distinzione tra i due concetti e indicato quale sia la corretta impostazione del problema sotto il profilo pedagogico. In quanto all'atteggiamento selettivo, non crediamo che esso possa essere posto in relazione con certi strumenti di verifica piuttosto che con altri, bensì riteniamo che esso debba essere collegato ad una visione globale della funzione della scuola nella società. Sappiamo bene che qualcuno, in particolari situazioni, cerca di avallare le proprie tesi sciorinando risultati di vari test: tenta cioè di far assurgere al rango di valutazioni i dati offerti da un mezzo di misurazione. A questo proposito occorre riaffermare la natura strumentale dei test: come ogni arnese funziona a dovere se si trova in mani esperte, così i test di profitto possono essere mezzi più efficaci — nei confronti delle prove tradizionali — solo se gli insegnanti che ne fanno uso sanno servirsene nell'ambito di una illuminata visione pedagogica, metodologica e didattica.